iStdDev 関数
この関数は、任意に設定したパラメータの標準偏差の値を計算して、その値を取得します。標準偏差はトレンド系のインジケータに分類されます。
標準偏差
標準偏差 (Standard Deviation) は、統計学においてデータのばらつきを表す指標の1つで、データの平均値からどれだけ離れているかを表します。集計したデータのばらつきが大きいほど、標準偏差の値は大きくなります。FXトレードでは、価格の変動幅を測る指標として使用されます。
標準偏差は統計学では σ (シグマ) の記号で表示されます。仮にばらつきの分布が正規分布になる場合は、ばらつきが±σの範囲に収まる確率は約68%になります。また、±2σの範囲に収まる確率は約95%、±3σの範囲に収まる確率は約99.7%になります。

この確率の考え方から 3σ以上になる確率は約0.3%しかなく、見ているデータのばらつきがこれまでより大きくなったとして何らかの変化が始まったと考えることができます。

MT4でチャート上に標準偏差をプロットする時はナビゲーター中のインディケータ → 「トレンド」 → 「Standard Deviation」インジケータを使用します。
(標準偏差の計算式)
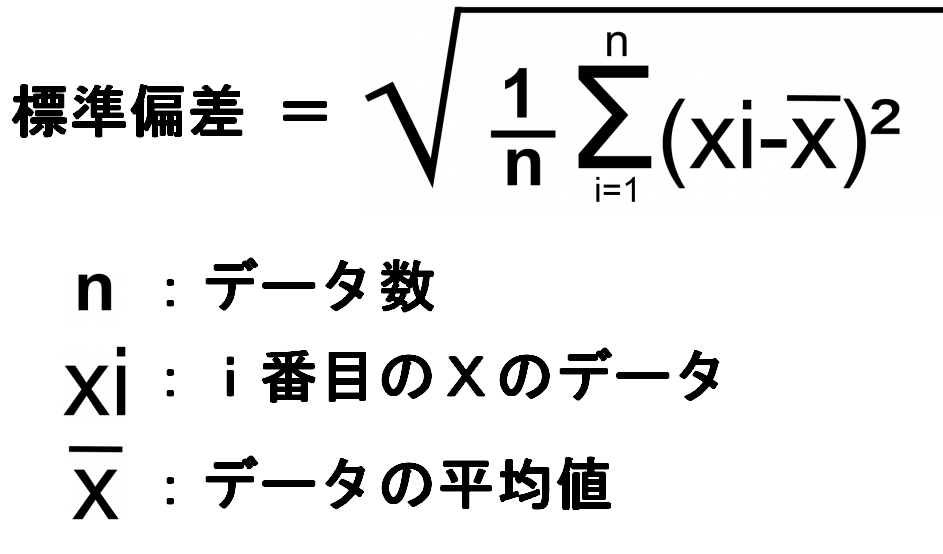
(標準偏差の使い方)
FXトレードにおいて、標準偏差は主にボラティリティ (変動幅) の指標として使われます。通常、短期的な価格変動のボラティリティを測定するために用いられます。
たとえば、ある通貨ペアの価格が直近の10日間で大きく動いている場合、標準偏差の値は高くなります。逆に、価格が比較的安定している場合、標準偏差の値は低くなります。
これにより、標準偏差は価格の変動を見極め、市場が過熱しているか、あるいは冷え込んでいるかを判断するのに役立ちます。また、トレンドの強さや逆転の可能性などを見る上でも有用です。
正規分布
正規分布とは、統計学において、多くの自然現象に現れる連続確率分布の一つであり、平均値を中心として左右対称に広がるベル型の曲線を描く確率分布のことです。正規分布に従うデータを生成することができる場合が多く、その性質から統計学や自然科学など多くの分野で広く用いられています。また、中心極限定理によって、独立な確率変数の和が正規分布に近づくことが知られており、多くの場合、現実世界で観測される現象の多くが正規分布に従うことが示唆されます。
データ型と構成・戻り値
double iStdDev(①, ②, ③, ④, ⑤, ⑥, ⑦);戻り値は、任意に設定したパラメータの標準偏差の値を計算して、その値を返します。
引数 [7]
iStdDev関数は 7個の引数で構成されます。
| 番 号 | 引数名 | データ型 | 単位 | 初期値 | 説明 |
|---|---|---|---|---|---|
| ① | symbol | string | - | - | 計算対象の通貨ペア名。 「NULL」は選択チャートの通貨ペア名が選択されます。 |
| ② | timeframe | int | - | - | 時間軸。ENUM_TIMEFRAMES 列挙値から選択。 「0」は現在チャートの時間軸が選択されます。 |
| ③ | ma_period | int | - | - | 標準偏差を計算する期間。標準偏差を計算するバーの数を数値で設定します。 |
| ④ | ma_shift | int | - | - | 移動平均シフト。チャートに対するインジケーターのシフトのことです。 |
| ⑤ | ma_method | int | - | - | 移動平均の方法。 ENUM_MA_METHOD 列挙値から選択。 |
| ⑥ | applied_price | int | 決済の 通貨単位 | - | 適用価格。 ENUM_APPLIED_PRICE 列挙値から選択。 |
| ⑦ | shift | int | - | - | 標準偏差を算出する位置。 現在のバーから指定した時間軸のバー数だけ過去へシフトします。たとえば、現在のバーからの計算は「0」、 1つ前のバーから計算する時は「1」になります。 |
使用例
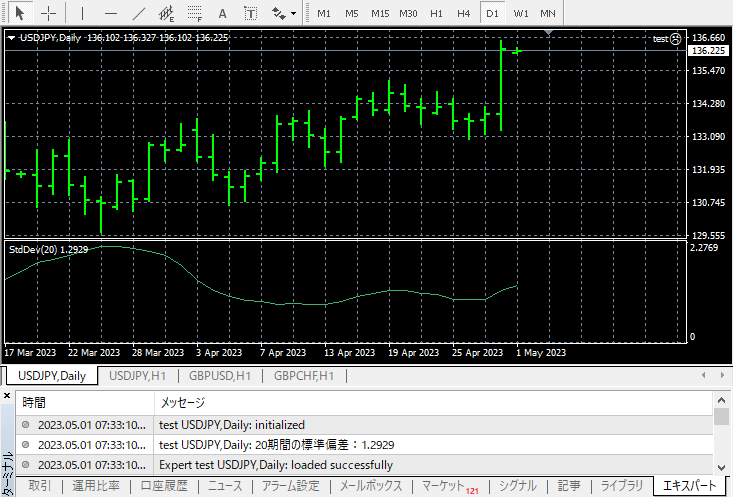
iStdDev関数による標準偏差値の計算
iStdDev関数を使って20日間分のバーの終値から標準偏差の値を算出します。
コード
// iStdDev関数による標準偏差値の計算
#property strict
void OnInit() {
int period = 20; // 期間
double a = iStdDev(NULL, 0, period, 0, 0, 0, 0);
Print(period, "期間の標準偏差値:", a);
}コードをコンパイルして実行する方法はこちらを参考にしてください。(デモ口座でお試しください)
結果